Getting Started With Music Theory
25 Feb 2023Introduction to Music - Part 1
Last month I tried understanding how music is written and communicated and I have to say, once you get to know the basics of music theory, the appreciation of good music increases exponentially. You can see what the musician just did that made you like it so much, why guitar players make weird finger pattern while playing. This is me just logging my understanding and taking notes to refer later on. If you understand music, do share your feedback.
Introduction
Musician figured out that sounds of what frequencies when played together or in a sequence with particular interval sounds good and what doesn’t. Most of the western music is created by dividing a range of frequency called an octave in 12 intervals of a fixed ratio defined by notes. Once the ratio of intervals between the notes is defined, same ratio can give you notes of higher or lower octave depending on where you start. So, if we start at 220Hz, we have one octave from 220 to 440Hz divided into 12 intervals by notes to reach 440Hz. And the next octave can start with 440Hz to 880Hz.
Piano or a keyboard is the best instrument to visualise this. Each key is a note and 12 keys (7 white, 5 black) keep repeating themselves from lower frequency octave to higher. You can go into how those interval ratio are decided but that would be too deep for this post.
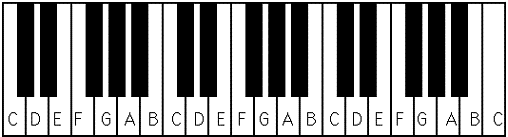
Source: http://www.piano-keyboard-guide.com/wp-content/uploads/2015/05/piano-keyboard-diagram.gif
Glossary
Octave: A range of frequency divided into 12 fixed ratio notes.
Note: Sound of a particular frequency, e. g., 220 Hz. (A to G)
Accidentals: Some of notes among 12 are called accidentals and named Sharp or Flat based on the notes preceding them or following them. On a keyboard, they are represented by black keys.
Semi Tone / Half Step: A semi tone (UK) or a half step (US) is a jump or interval of 1 note, e.g. half step from C would take you to C# and half step from C# would take you to D.
Full Tone / Tone / Whole Step / Step: A whole step is a jump of 2 notes, e.g. a whole step from C would take you to D (skipping a c# in between) and from E to F#.
Key and Scale: Not to confuse with keyboard key, in music theory, key is a note on which the pattern i.e. the next set of notes, is defined. And the pattern is called the scale. Most popular scales are major, minor, diminished and augmented. For example, C Major would mean a major scale pattern or sequence of notes based on key of C.
Interval: Two notes from a scale or sequence represents an interval, e.g, 2nd interval would be 2nd note of the scale, 3rd interval would be 3rd note of the scale with respect to the first note called root. Interval is relative, so if root is moved up by a step, then 2nd, 3rd and all other intervals would also move up by a step.
Chord: Three or more notes from a sequence of notes (scale) played together is a chord.
Triad: A **Chord with exactly 3 alternate notes from a scale, i.e., root - 3rd interval - 5th interval
Degree of Chord: Degree defines where to start the chord on a scale, e.g. 3rd degree triad of a C major scale would start from 3rd note of the scale and contain 5th and 7th note.
Melody: Chords played along with other notes.
Notes
Music theory divides these notes as pure and accidental. Seven Pure denoted by English alphabets - A, B, C, D, E, F, G and five accidentals denoted by # (sharp) or b (flat) relative to pure note e.g. note between A and B is called A# or Bb. In keyboard, white keys are pure notes (repeating from A to G) and black keys are accidentals notes represented in terms of pure note so, black key between C and D can be called C# or Db. So 12 notes would be — A, A#/Bb, B, C, C#/Db, D, D#/Eb, E, F, F#/Fb, G, G#/Cb. Notice that there is no B# and E#, this is the way intervals are defined by musicians, if you find out the reasoning, I would love to hear it 🤔.
In keyboard, the accidentals are fitted in between pure keys while guitar doesn’t have that distinction, this might have to do something the way instruments are played i.e. to make the whole octave reachable for one hand 🤷.
Major and Minor Scales
Musicians have defined a scales as sequence of notes or relative steps from a key. For Major scales of a key, steps are defined as - Whole Whole Half Whole Whole Whole Half. So a C Major scale would be, referring keyboard image above while taking the whole or half step — C D E F G H A B, i.e. all white keys of the keyboard.
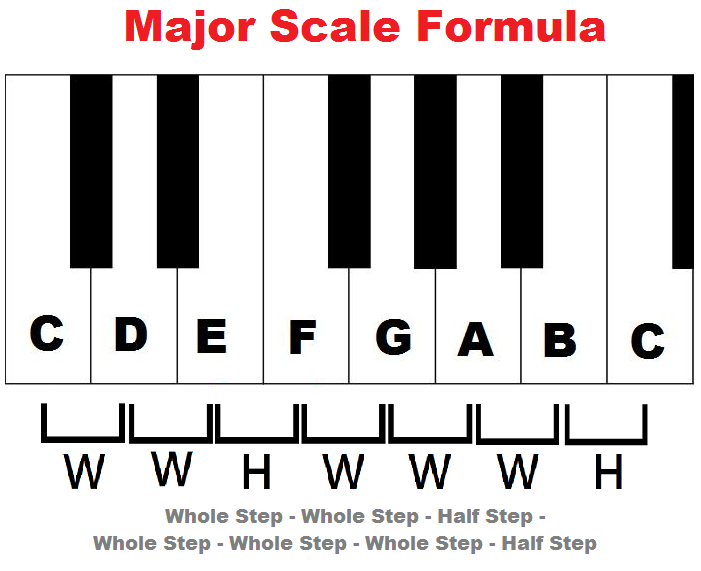
Source: http://www.piano-keyboard-guide.com/wp-content/uploads/2015/05/major-scale-formula.png
Similarly, for a minor scale of a key the sequence of steps is defined as — Whole Half Whole Whole Half Whole Whole. So the notes of C Minor scale would be C D Eb F G Ab Bb C. Notice that 2nd, 4th and 5th intervals have the same note for major and minor scale.
🎵 Mojor Scale Steps - W W H W W W H
Minor Scale Steps - W H W W H W W
A chord on a scale can also be defined as major or minor depending on which scale the 3rd interval is falling, as the 5th is going to be same in major or minor. So 4th degree chord or triad on C Minor scale is F Ab C which would be called a F Minor chord (Fm) as it starts with F and 3rd is falling in minor scale of F and 2nd degree triad on C Major scale is D F A which would be a D Minor (Dm) as it starts with D and 3rd is falling on minor scale of D.
💡 Now, since 5th is same in a major and minor scale and 3rd of a minor scale is 3 half steps away from root and 3rd of a major scale is 4 half steps away, you can get a major triad by taking 4 then 3 half steps from root and minor triad by ?> taking 3 then 4 half steps.
💡 In other words, you can get a minor from a major chord by lowering a half step on the 3rd interval and minor chord by raising the 3rd interval by a half step. For example, Dm is
D F Aand D major chord (written as just D) would beD F# A.
Degree and Chords Notation
The degree of the chord is represented by a roman number and if it’s major then the capital roman number while minor chord would be written as small roman number.
For example, we’ll write chords or triads (root, 3rd and 5th) of C Major scale (C D E F G A B C) with different degree. Remember, If the chord has 3rd and 5th with 4 steps then 3 steps from root, it’s major chord and minor if 3rd and 5the are 3 step then 4 step away from the root.
| Degree | Notes | Chord | Notation |
|---|---|---|---|
| 1st degree | C E G | C Major (C) | I |
| 2nd degree | D F G | D Minor (D) | ii |
| 3rd degree | E G B | E Minor (Em) | iii |
| 4th degree | F A C | F Major (F) | IV |
| 5th degree | G B D | G Major (G) | V |
| 6th degree | A C E | A Minor (Am) | vi |
7th degree triad gives something called a diminished chord which is denoted by a naught superscript to the roman number (vii), we’re ignoring this for now. And similarly, 1-7 degree chords of A Minor scale (A B C D E F G A) would be - Am, B diminished, C, Dm, Em, F, G and denoted as i, ii, III, iv, v, VI, VII.
Not that we’re clear of popular pattern of frequencies that are used to play music, there is time aspect to it as well. The series of notes follows a certain rhythm or time gap between the tones, understanding that would allow to communicate the speed of music notes in which they should be played.
Rhythm
Rhythm guides the music notes with respect to time, i.e., when to play the subsequent notes of a pattern and for how long before playing another note or taking rest. It gives a pattern of tone and rests in terms of beat. The basic unit of rhythm can be set against time by setting beats per minute (BPM), so same notes can be played slow or fast in time but the rhythm remains same. For example, 30 bps would mean 1 beat every 2 seconds while 60 bps is 1 beat per second. 4 beats makes a measure or bar and represents a whole note so if a note is played every beat then it’s quarter note i.e. 4 notes in a measure. If 2 notes are played with every beat i.e. 8 notes per measure then that would be a eighth note. And if there are 4 notes every beat, then it’s a sixteenth note and a measure would have 16 notes. You can keep dividing the beat, but these are the most popular ones.
To count or write notes in time i.e. beat, popular notation is -
| Note | Measure |
|---|---|
| Quarter | 1 2 3 4 |
| Eighth | 1 & 2 & 3 & 4 & |
| Sixteenth | 1 e & a 2 e & a … |
Reference - Found this explanatory video by Andrew Huang very helpful.
– Nikhil